A. Extensions (uzaytirgichlar)

Xotira: 512 MB, Vaqt: 1000 ms

Masala

Nodir o’tgan o’quv yilida \(N\) ta olimpiadada qatnashdi va har birida bittadan uzaytirgich (pilot) yutib oldi. Bunda \(i\) - uzaytirgichda \(a[i]\) ta rozetkasi bor.

Shuningdek, Nodirda cheksiz ko’p miqdorda telefonlar bor. Har bir telefonni quvvatlantirish uchun unga bittadan rozetka kerak, biroq Nodirning uyida energiya manbai bitta.

Uzaytirgichlarni bir-biriga shunday tartibda ulangki, bunda energiya manbalarini soni maksimal bo’lsin va iloji boricha ko’proq telefonni quvvatlantirsin.

Kiruvchi ma'lumotlar:

Birinchi qatorda sizga \(N\) soni beriladi - jami uzaytirgichlar soni.

Ikkinchi qatorda \(a[1], \space a[2], \space \dots, \space a[N]\) - uzaytirgichlardagi rozetkalar soni.

Chegaralar:

• \(1 ≤ N ≤ 10^5\)

• \(2 ≤ a_i ≤ 100\), barcha \(1 ≤ i ≤ N\) uchun

Subtasklar:
1. (15 ball) \(N = 1\)
2. (20 ball) \(N ≤ 8\)
3. (20 ball) \(a[1] = a[2] = ... = a[N]\).
4. (45 ball) Qo’shimcha chegaralarsiz.

Chiquvchi ma'lumotlar:

Yagona qatorda ko’pi bilan nechta telefonni quvvatlantish mumkinligini chiqaring.

Izoh:

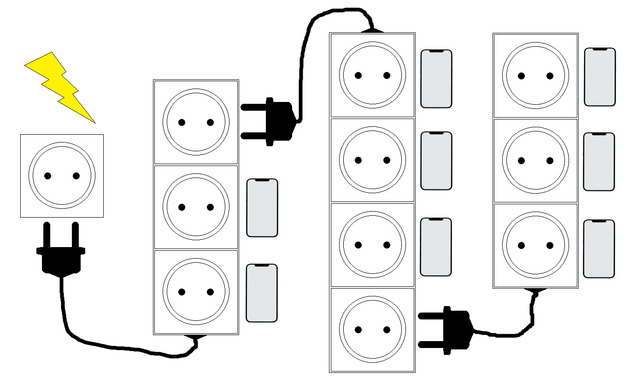
Masalan, \(N = 3\) va \(a = [3, 3, 4]\) bo’lsin.

Agar Nodir uzaytirgichlarni \([3, 4, 3]\) tartibida ulasa 8 ta telefonni quvvatlantira oladi.

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	3 3 3 4	8

B. Fruits (Mevalar)

Xotira: 512 MB, Vaqt: 1000 ms

Masala

Gavhar o’zining super bog’idan \(N\) dona meva terib oldi va bir qatorga terib chiqdi. Har bir meva bu yoki Apelsin yoki Banan. Gavharga apelsin ko’proq yoqadi, shuning uchun u shunday mevalar oralig’ini tanlamoqchiki, bunda chapdan kelganda ham, o’ngdan kelganda ham Apelsinlar soni har doim Bananlar sonidan kam bo’lmasligi kerak.

Bunday oraliqlar ichidan Gavhar uzunligi maksimalini tanlamoqchi. Siz unga yordam bering!

Kiruvchi ma'lumotlar:

Birinchi qatorda sizga \(N\) soni beriladi, mevalar soni.

Ikkinchi qatorda uzunligi \(N\)ga teng \(S\) satr. Bunda har bir element yoki \(a\) (apelsin),
yoki \(b\) (banan)ga teng.

Chegaralar
• \(1 ≤ N ≤ 10^6\)
• \(S\) satr faqat \(A\) va \(B\) belgilaridan tashkil topgan

Subtasklar
1. (11 ball) \(N ≤ 300\)
2. (17 ball) \(N ≤ 2000\)
3. (19 ball) \(N ≤ 5000\)
4. (10 ball) \(N ≤ 10^5\) , shuningek avval faqat apelsinlar, keyin faqat bananlar, va so’ngida faqat apelsinlar bor.
5. (22 ball) \(N ≤ 10^5\)
6. (21 ball) Qo’shimcha chegaralarsiz

Chiquvchi ma'lumotlar:

Yagona qatorda eng uzun oraliqning uzunligini chiqaring.

Izoh:

Masalan, N = 8 va S = “baaababb” bo’lsin. Biz S[2...6] = “aaaba” oraliqni tanlashimiz mumkin.

Chapdan o’ngga kelganimizda satr “aaaba” bo’ladi.
Bunda “a”, “aa”, “aaa”, “aaab” va “aaaba” satrlarning har birida “a”lar soni “b”lar sonidan kam emas.

O’ngdan chapga kelganimizda satr “abaaa” bo’ladi.
Bunda “a”, “ab”, “aba”, “abaa” va “abaaa” satrlarning har birida “a”lar soni “b”lar sonidan kam emas.

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	8 baaababb	5

C. Aliens (O'zga sayyoraliklar)

Xotira: 512 MB, Vaqt: 4000 ms

Masala

Gulnozaning \(N × M\) o’lchamli bog’i bor. Agar \(a[i][j] = “T”\) bo’lsa \((i, j)\) katakda daraxt bor, aks holda katak bo’sh.

Gulnozaning ukasi Yahyo esa koinotga juda ham qiziqadi va u o’zga sayyoraliklarga romb ko’rinishida xabar jo’natmoqchi. Buning uchun u bog’ning bir-nechta kataklariga toshlar o’rnatib chiqishi mumkin. Toshlar yuqoridan qaraganda romb ko’rinishini hosil qilishi lozim. Biroq Yahyo daraxtlarga ziyon yetkazmoqchi emas (Daraxtlarni asrang!).

Xabar qanchalik katta bo’lsa, o’zga sayyoraliklar uni qabul qilish ehtimoli shunchalik ortadi. Iloji boricha ko’p tosh qo’yish orqali romb yarating!

Kiruvchi ma'lumotlar:

Birinchi qatorda sizga \(N\) va \(M\) beriladi, Gulnozaning bog’ining o’lchamlari.

Keyingi \(N\)ta qatorda \(M\)tadan belgi, bunda “\(T\)” - daraxtni bildirsa, “\(.\)” - bo’sh katakni bildiradi.

Chegaralar
• \(3 ≤ N, M ≤ 5 000\)
• \(a[i][j] = “T”\) yoki “\(.\)”, barcha \(1 ≤ i ≤ N\) va \(1 ≤ j ≤ M\) uchun
• Kamida bitta katak bo’sh ekanligi kafolatlanadi.

Subtasks
1. (10 ball) \(N = M = 3\)
2. (11 ball) \(N, M ≤ 30\)
3. (12 ball) \(N, M ≤ 100\)
4. (13 ball) \(N, M ≤ 400\)
5. (17 ball) \(N, M ≤ 1000\) va ko’pi bilan 10ta daraxt bor
6. (14 ball) \(N, M ≤ 1000\)
7. (23 ball) Qo’shimcha chegaralarsiz

Chiquvchi ma'lumotlar:

Yagona qatorda ishlatish mumkin bo’lgan maksimal toshlar sonini chiqaring.

Izoh:

Masalan, \(N = 7\) va \(M = 6\) bo’lsin. Maydonda 7 ta daraxt bor va ularga ziyon yetkazmasdan 13 ta toshni romb ko’rinishida joylashtirish mumkin.

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	7 6 .T...T ..T... T....T ...... T..... ...... ...T..	13

D. Product (Ko’paytma)

Xotira: 512 MB, Vaqt: 1400 ms

Masala

Gavhar kiyim do’konidan so’ng sonlar do’konini ham ochdi. Do’konda \(i\)-sonning qiymati \(a[i]\) ga teng va narxi \(c[i]\) so’m turadi.

Umidning sevimli soni \(T\)ga teng. Umid do’kondan bir-nechta sonlarni sotib olmoqchi, bunda ularning ko’paytmasi \(T\)ga teng bo’lishi, umumiy narxi esa minimal bo’lishi zarur. Umidga yordam bering.

Kiruvchi ma'lumotlar:

Birinchi qatorda sizga \(N\) va \(T\) sonlari beriladi.

Ikkinchi qatorda \(a[1], a[2], ..., a[N]\) - sonlarning qiymati.

Uchinchi qatorda \(c[1], c[2], ..., c[N]\) - sonlarning narxi.

Chegaralar

• \(1 ≤ N ≤ 10^5\)
• \(2 ≤ T ≤ 10^9\)
• \(1 ≤ a[i] ≤ 10^9\) , barcha \(1 ≤ i ≤ N\) uchun
• \(1 ≤ c[i] ≤ 10^9\) , barcha \(1 ≤ i ≤ N\) uchun

Subtasks

1. (12 ball) \(N ≤ 18\)
2. (13 ball) \(N ≤ 100\), \(T ≤ 100\)
3. (20 ball) \(N ≤ 1000\), \(T ≤ 1000\).
4. (11 ball) \(T = 2^x\) , bunda \(x\) - musbat butun son.
5. (29 ball) \(C[i] = 1\), barcha \(1 ≤ i ≤ N\) uchun
6. (15 ball) Qo’shimcha chegaralarsiz

Shuningdek, har bir subtaskda, agar minimal narxni topib, aynan qaysi sonlarni sotib olish kerakligini chiqarmasangiz, shu subtask ballarini 70% miqdorini qo’lga kiritasiz. Bunda javobda \(k = 0\) chiqarishingiz kerak, ya’ni:
\(C \space 0\)

Chiquvchi ma'lumotlar:

Agar ko’paytmani \(T\)ga tenglashtirishning iloji yo’q bo’lsa, yagona qatorda \(−1\) chiqaring. Aks holda:

Birinchi qatorda \(C\) - minimal narx, \(k\) - tanlangan elementlar soni.

Ikkinchi qatorda \(b[1], b[2], ..., b[k]\) - tanlangan sonlar indekslari.

Bunda \(1 ≤ b[1] < b[2] < ... < b[k] ≤ N\) bo’lishi, \(a[b[1]] \times ... \times a[b[k]] = T\) va \(c[b[1]] + ... + c[b[k]] = C\) bo’lishi talab e’tiladi.

Agar minimal narxda sotib olish variantlari ko’p bo’lsa, ulardan ixtiyoriysini chiqarishingiz mumkin.

Izoh:

Masalan, \(N = 6\), \(a = [2, 3, 6, 7, 2, 1]\), \(c = [1, 4, 9, 1, 3, 1]\) va \(T = 12\) bo’lsin. Agarda Umid 1, 2, va 5-o’rindagi sonlarni sotib olsa \(a[1] · a[2] · a[5] = 2 · 3 · 2 = 12\) bo’ladi va \(c[1] +c[2] +c[5] = 1 + 4 + 3 = 8\) so’m bo’ladi.

Ikkinchi misolda ko’paytmani 18ga tenglashtirishning iloji yo’q. Shuning uchun javobda −1 chiqarish kerak.

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	6 12 2 3 6 7 2 1 1 4 9 1 3 1	8 3 1 2 5
2	4 18 3 2 2 4 9 2 7 5	-1

E. MEX-xe-xe

Xotira: 1024 MB, Vaqt: 2000 ms

Masala

Nodir, Gavhar, Gulnoza, Yahyo va Umid birgalikda NGGYU™ kompaniyasiga asos solishdi. Kompaniyaning asosiy ustuvorlik vazifasi MEX haqida masala ishlash.

MEX - Minimum Excluded, massivda yo’q bo’lgan eng kichkina nomanfiy butun son. Masalan \(\text{MEX}([1, 2, 0, 5]) = 3 \)va \(\text{MEX}([1, 3]) = 0\).

Sizga \(N\)ta elementdan iborat \(a[1], a[2], ..., a[N]\) massiv berilgan.

Berilgan \(k\) son uchun, \(a\) massivni bir-nechta bo’laklarga bo’lishingiz mumkin. Agar har bir bo’lakning \(\text{MEX}\) qiymati \(k\)dan oshmasa, u holda bu ajratish yaxshi deyiladi. \(f(k)\) deb, yaxshi ajratishdagi minimal bo’laklar soniga aytiladi.

Barcha \(1 ≤ k ≤ N\) uchun \(f(k)\) qiymatini toping.

Kiruvchi ma'lumotlar:

Birinchi qatorda sizga \(N\) soni beriladi.
Ikkinchi qatorda \(a[1], a[2], ..., a[N]\).

Chegaralar
• \(1 ≤ N ≤ 10^6\)
• \(0 ≤ a[i] < N\), barcha \(1 ≤ i ≤ N\) uchun

Subtasks
1. (7 ball) \(N ≤ 100\)
2. (7 ball) \(N ≤ 1000\)
3. (7 ball) \(N ≤ 3000\)
4. (7 ball) \(N ≤ 5000\).
5. (7 ball) \(N ≤ 10 000\).
6. (7 ball) \(N ≤ 20 000\).
7. (7 ball) \(N ≤ 30 000\).
8. (7 ball) \(N ≤ 40 000\).
9. (9 ball) \(N ≤ 100 000\).
10. (7 ball) \(N ≤ 150 000\).
11. (7 ball) \(N ≤ 250 000\).
12. (7 ball) \(N ≤ 350 000\).
13. (7 ball) \(N ≤ 500 000\).
14. (7 ball) Qo’shimcha chegaralarsiz.

Chiquvchi ma'lumotlar:

Yagona qatorda \(N\)ta butun son - \(f(1), f(2), ..., f(N)\) chiqaring

Izoh:

Masalan, \(N = 8\) va \(a = [0, 1, 1, 2, 0, 2, 1, 0]\) bo’lsin.

\(f(1) = 5\), chunki massivni \([0]; [1, 1, 2]; [0, 2]; [1]; [0]\) qilib 5 ta bo’lakka bo’lishimiz mumkin.

\(f(2) = 3\), chunki massivni \([0, 1, 1]; [2, 0, 2]; [1, 0]\) qilib 3 ta bo’lakka bo’lishimiz mumkin.

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	8 0 1 1 2 0 2 1 0	5 3 1 1 1 1 1 1