A. Toq yoki juft
Xotira: 32 MB, Vaqt: 1000 msIkki son berilgan. Sonlarning yig'indisi toq yoki juft ekanligini aniqlang.
Birinchi qatorda ikkita son A va B berilgan.
\(1 \le A, B \le 10^{100000}\)
Agar yig'indi toq bo'lsa “toq”, aks holda “juft” so'zini chop eting.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
5 6 |
toq |
| 2 |
4 4 |
juft |
| 3 |
6967936668 3830121 |
toq |
B. Iplar
Xotira: 256 MB, Vaqt: 1000 msFarruxga akasi Shohruh n ta ipdan tashkil topgan to'plamni berdi. Iplar bir qatorda ketma-ket joylashtirgan. Farrux ikkita yonma-yon ipni bir-biriga ulashi mumkin. Shunda iplar soni 1 taga kamayadi.
Farrux barcha iplarni kamida \(w\) uzunlikda bo'lishini xohlaydi. Bu ishni amalga oshirgandan so'ng maksimum nechta dona ip qolishi mumkin?
Birinchi qatorda \(n\) va \(w\) iplar soni va Farrux xohlayotgan minimum uzunlik kiritiladi.
Keyingi qatorda \(n\) ta butun son \(a_i\) - har bir ipning uzunligi kiritiladi.
\(1 \le n, w \le 10^6\)
\(1 \le a_i \le 10^6\)
Barcha iplarning uzunligi kamida \(w\) bo'lgandan keyin qolishi mumkin bo'lgan iplarning maksimal sonini chop eting.
Agar barcha iplarning uzunligi yig'indisi \(w\) dan kichik bo'lsa, 0 ni chop eting.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
7 4 1 2 3 4 3 1 1 |
3 |
C. Mebel xarid qilish
Xotira: 32 MB, Vaqt: 1000 msZarif mebellarni onlayn xarid qiladi. U allaqachon chiroyli stol va stullar to'plamini topib olgan edi. Endi u stol atrofiga sig‘ishi uchun qancha stul sotib olish mumkinligini o'ylayapti.
Stol \(N \times M\) o'lchamdagi to'g'ri to'rtburchak shaklida, stullar esa \(K \times K\) o'lchamdagi kvadrat shaklida.
Har bir stul stol yoniga suyanchiq bilan qo'yilishi kerak, ya'ni suyanchig'i bilan chekkasi stolning ma'lum bir chetiga to'g'ri kelishi kerak. Bundan tashqari, o'rindiq butunlay stol ichida joylashgan bo'lishi kerak. Albatta, ikkita stul bir-biriga ustma-ust tushmaydi. Biz stol oyoqlarini e'tiborsiz qoldiramiz (biz ular cheksiz nozik va stol usti burchaklarida joylashgan deb taxmin qilishimiz mumkin). Stol ostiga nechta stul sig'adi?
Birinchi qatorda 3 ta butun son \(N, M, K\) kiritiladi.
\(1 \le N, M, K \le 10^9\)
Maksimal stullar sonini chop eting.
Birinchi test holati uchun yechim:
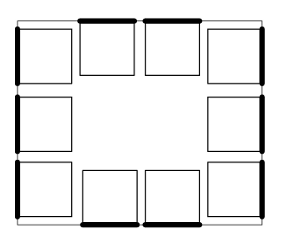
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
15 18 4 |
10 |
| 2 |
12 8 4 |
6 |
D. Kimyoviy tajriba
Xotira: 256 MB, Vaqt: 1000 msAtomlar 2 xil bo'ladi: zaryadlangan yoki zaryadsiz. Agar atom zaryadlangan bo'lsa, ular ionlar deb ataladi. Har bir ion butun qiymatga ega zaryadlangan bo'ladi. Agar zaryad manfiy bo'lsa anion, aks holda kation deyiladi.
Farrux va Doniyor kimyoviy tajriba o'tkazishmoqda.
Farrux anionlar va zaryadsiz atomlardan iborat idish tayyorladi. Biz bu idishni to'rtburchaklar sonlar tarmog'i sifatida ko'rsatamiz, bu yerda \(-x\) manfiy raqam zaryadli anionni va nol zaryadsiz atomni ifodalaydi.
Keyin Doniyor kationlarni idishga birma-bir soladi va keyingi kationni kiritishdan oldin joriy kation anion bilan muvaffaqiyatli bog'lanishini kutadi.
Farrux va Doniyor ular o'rganayotgan maxsus atomlar va molekulalar uchun zaryadli kation zaryadli bitta erkin anion bilan bog'lanishini bashorat qilmoqdalar. To'g'ri miqdorda zaryadlangan bir nechta bo'sh anionlar bo'lsa, kation to'rtburchaklar idishda eng yuqori bo'lgan anion bilan bog'lanadi. Agar hali ham eng yuqori bo'lgan bir nechta erkin anionlar mavjud bo'lsa, kation eng chapdagi bilan bog'lanadi. Kation anion bilan bog'langandan so'ng, ikkala ion ham zaryadsizlanadi va boshqa kimyoviy o'zaro ta'sirlarda qatnashmaydi.
Kafolatlanganki, Doniyor har bir kation bilan bog'lanishi mumkin bo'lgan mos keladigan anionga ega bo'ladigan tarzda idishga kationlarni kiritadi.
Farrux va Doniyor o'zlarining bashoratlari to'g'ri yoki yo'qligini bilish uchun tajribalarining kompyuter simulyatsiyasini yaratmoqchi. Farrux anion idishining to'liq tavsifi va Doniyorning idishga kiritadigan kationlar ketma-ketligini hisobga olib, agar tajriba ularning bashoratiga ko'ra harakat qilsa har bir kation qaysi anion bilan bog'lanishi kerakligini aniqlamoqchi. Ularga yordam bera olasizmi?
Birinchi qatorda N va M - idishning bo'yi va eni kiritiladi.
Keyingi N ta qatorning har birida M tadan son kiritiladi. Bu idishning konstruksiyasini ifodalaydi. Barcha sonlar 0 dan katta emasligi kafolatlanadi.
Keyingi qatorda Q ta son - Doniyordagi kationlar soni kiritiladi.
Keyingi Q ta qatorning har birida bittadan natural son kiritiladi. Har bir kationga mos keladigan anion borligi kafolatlanadi.
\(1 \le N, M \le 10^3\)
\(1 \le Q \le 2 \times 10^5\)
Kation va anionlarning absolyut qiymati \(2 \times 10^5\) dan oshmasligi kafolatlanadi.
Har bir kation uchun mos keluvchi anion turgan joyni chop eting.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
3 3 0 -2 -2 -3 0 0 -3 0 -1 5 3 2 1 3 2 |
1 0 0 1 2 2 2 0 0 2 |
| 2 |
3 3 0 -2 0 -3 0 0 0 0 -1 3 1 2 3 |
2 2 0 1 1 0 |
E. DTM
Xotira: 512 MB, Vaqt: 3000 msBir necha kundan so'ng davlat imtihonlari boshlanadi. DTM (Davlat Test Markazi) tomonidan abiturientlarga qulaylik yaratish uchun ketma-ket n kun davomida har kuni namunaviy test materiallari ishlanadi. DTM tomonidan k ta test tuzilgan va 1 dan k gacha raqamlangan. Shahzoda ham abiturient va u ham testlarni ishlab ko'rmoqchi. Shahzoda \(a_i\) raqamli variantni ishlasa, uning kayfiyati \(b_{a_i}\) ga ortadi. Biroq bitta testni ikki yoki undan ko'p marta ishlasa, hech qanday kayfiyat olmaydi: ushbu testdan olgan umumiy kayfiyati 0 ga teng bo'ladi. Shahzoda testni istalgan kunda boshlashi va tugatishi mumkin, lekin ushbu oraliqdagi birorta kunni o'tkazib yuborishi mumkin emas. Shahzoda eng ko'pi bilan qancha kayfiyatga ega bo'lishi mumkin? (Boshlang'ich kayfiyat 0 ga teng deb hisoblang)
Birinchi qatorda n va k - kunlar va variantlar soni kiritiladi.
Keyingi qatorda n ta butun son - \(a_i\) har bir kunda ishlanadigan test varianti raqami kiritiladi.
Keyingi qatorda k ta butun son - \(b_i\) har bir test Shahzodaning kayfiyatini qanchaga o'zgartirishi kiritiladi.
\(1 \le k \le n \le 10^6\)
\(1 \le a_i \le k\)
\(1 \le b_i \le 10^6\)
Shahzoda olishi mumkin bo'lgan maksimal kayfiyatni chop eting.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
10 5 2 4 1 1 2 3 2 2 2 3 14 7 13 16 10 |
37 |