A. P! = 0 (mod 10N)
Xotira: 16 MB, Vaqt: 1000 msSizga bitta butun N soni beriladi, siz P! = 0 (mod 10N) shartni qanoatlantiradigan eng kichik P natural sonni toping. Bu yerda ! belgisi faktorialni ifodalaydi.
Kirish faylining dastlabki satrida bitta butun son, T(1 ≤ T ≤ 105) testlar soni kiritiladi. Keyingi T ta qatorda bittadan butun son, N(1 ≤ N ≤ 109) soni kiritiladi.
Har bir test uchun alohida qatorda bittadan butun son, P! = 0 (mod 10N) shartni qanoatlantiruvchi eng kichik P natural sonni chop eting.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
4 1 2 3 4 |
5 10 15 20 |
B. Number game
Xotira: 16 MB, Vaqt: 1000 msDasturchilar Klubining a’zosi Azimjon sonlar bilan bo’gliq o’yinlarga juda qiziqadi. Bir kuni Azimjon do’sti Maqsud bilan ajoyib o’yin oynamoqchi bo’ldi. Azimjon o'zi o’ylagan a sonini Maqsud o’ylagan b soniga aylantirish uchun quyidagi amallarni bajarishini aytdi.
- Sondan 1 ni olib tashlash.
- 2 dan k gacha bo'lgan har qanday butun x sonini tanlab, a sonidan (a mod x) ayirish.
(a mod x) operatsiyasi - a sonini x soniga bo'lganda qolgan qildiqni anglatadi.
Azimjon bir soniyada yuqoridagi amallardan birini bajaradi va u o’ylagan a soni ham o’zgarib boraveradi. U o’zining oylagan soni Maqsudning soniga aylanmaguncha, har soniyada o’zi istagan amallardan birini bajaraveradi. Azimjon juda aqilli dasturchi bo’lgani uchun, bu ishni eng kam vaqtda bajaradigan dastur yordamida amalga oshirmoqchi. Siz ham Azimjonga yordam berishga urinib ko’ring
E'tibor bering: ikkinchi amaldagi x raqamlari har safar bir-biridan mustaqil ravishda yangidan tanlanadi.
Bitta qatorda Azimjon o’ylagan son, Maqsud o’ylagan son va \(k\) soni. \((1 ≤ b ≤ a ≤ 10^{18} ; 2 ≤ k ≤ 15)\).
Azimjon eng kamida necha soniya ichida o’z sonini Maqsud o’ylangan songa aylantirishini aniqlang.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
8 2 3 |
4 |
| 2 |
15 10 5 |
2 |
| 3 |
10 1 4 |
6 |
C. Massiv bo’laklari
Xotira: 64 MB, Vaqt: 2000 msUzunligi N ga teng bo’lgan A massiv berilgan. Biz berilgan massivni bir nechta bo’laklarga bo’lib, bo’laklardan B massivni hosil qilishimiz mumkin. Misol uchun agar A = [1, 2, 3] ga teng bo’lsa, biz uni B massivga quyidagi ko’rinishlarda bo’laklab berishimiz mumkin:
- B = [(1), (2), (3)]
- B = [(1, 2), (3)]
- B = [(1), (2, 3)]
- B = [(1,2,3)]
Bitta bo’lakning qiymati (bo’lakdagi elementlar yig’indisi) * (bo’lak elementlari soni) ga teng. B massivning qiymati esa undagi barcha bo’laklarning qiymatlari yig’indisiga teng.
Sizga A massiv berilgan, siz hosil qilinishi mumkin bo’lgan barcha B massivlarining umumiy qiymatini toping. Misol uchun yuqoridagi A = [1, 2, 3] da:
[(1), (2), (3)] ning qiymati 1 * 1 + 2 * 1 + 3 * 1 = 6
[(1, 2), (3)] ning qiymati 3 * 2 + 3 * 1 = 9
[(1), (2, 3)] ning qiymati 1 * 1 + 5 * 2 = 11
[(1, 2, 3)] ning qiymati 6 * 3 = 18
Sizning javobingiz 6+9+11+18 = 44 ga teng bo’lishi kerak.
Kirish faylining dastlabki satrida bitta butun son, N(1 <= N <= 106), A massiv elementlari soni kiritiladi.
Ikkinchi satrda N ta butun son, A (1 <= Ai <= 109) massiv elementlari kiritiladi.
Chiqish faylida yagona butun son, natijaning 109+7 (1000000007) ga bo’lgandagi qoldig’ini chop eting.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
3 1 3 6 |
73 |
| 2 |
5 4 2 9 10 1 |
971 |
D. Qismlarga bo'lish o'yini
Xotira: 16 MB, Vaqt: 1000 msMirzo Ulug’bek kitob olgani kitob do’koniga bordi. Ming afsuski uning hamyonida birorta ham kitobga yetadigan puli yo’q edi. Buni chetdan kuzatib turgan kitobxona xo’jayini Mirzo Ulug’bekning kitobga qiziqishini ko’rganidan so’ng Mirzo Ulug’bekka kitob sovg’a qilish maqsadida unga o’yin o’ynashni taklif qildi, shu o’yinda Mirzo Ulug’bek necha ball yig’sa, shuncha kitobni sovg’a qilishini aytdi. Tabiiyki Mirzo Ulug’bek bunga ko’ndi va diqqat bilan o’yin shartlarini tingladi:
- Mirzo Ulug’bekga nomanfiy butun sonlardan iborat massiv beriladi.
- Mirzo Ulug’bek massivni ketma-ket elementlardan tashkil topgan, bo’sh bo’lmagan shunday 2 massivga ajratishi kerakki chap tomon elementlaridan tashkil topgan massiv elementlari yig’indisi o’ng tomon elementlaridan tashkil topgan massiv elementlari yig’indisiga teng bo’lishi kerak. Agar Mirzo Ulug’bek bu ishni amalga oshira olsa u 1 ball ga ega bo’ladi, aks holda o’yin o’z nihoyasiga yetadi.
- Har bir muvoffaqiyatli turdan so’ng Mirzo Ulug’bek chap yoki o’ng tomon elementlaridan tashkil topgan massivni o’yindan tashqariga uloqtiradi va o’zida qolgan massiv bilan o’yinni davom ettiradi.
Masalan: dastlab Mirzo Ulug’bekda \([1,2,3,6]\) massivi mavjud bo’lsin, u bu massivni \([1,2,3]\), \([6]\) shaklida ikkiga taqsimlashi mumkin(+1 ball), shundan so’ng \([6]\) ni o’yindan chiqarib, o’yinni \([1,2,3]\) bilan davom ettiradi. U bu massivni \([1,2]\), \([3]\) shaklida ikkiga taqsimlashi mumkin(+1 ball), shundan so’ng \([3]\) ni o’yindan chiqarib, o’yinni \([1,2]\) bilan davom ettiradi. U bu massivni ikkiga taqsimlay olmaydi va o’yin nihoyasiga yetib Mirzo Ulug’bek 2 ball ga ega bo’ladi, ya’ni kitob do’konidan ixtiyoriy 2 ta kitobni tekinga olib ketishi mumkin bo’ladi.
Dastlabki satrda bitta butun son, \(T(1 ≤ T ≤ 10)\) testlar soni kiritiladi. Keyingi satrdan boshlab har bir test uchun alohida ikkita satrning birinchi satrida \(N(1 ≤ N ≤ 2^{14})\) – massiv elementlari soni, ikkinchi satrida \(N\) ta \([0, 10^9]\) oralig’idagi butun son, ya’ni, Mirzo Ulug’bekdagi dastlabki massiv elementlari kiritiladi.
Har bir test uchun alohida qatorda bittadan butun son, Mirzo Ulug’bek kitob do’konidan ko’pi bilan nechta kitobni tekinga olib ketishini chop eting.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
5 4 1 2 3 6 4 1 2 6 3 3 3 3 3 4 2 2 2 2 7 4 1 0 1 1 0 1 |
2 0 0 2 3 |
E. Ko’pburchaklarni bo’lish
Xotira: 64 MB, Vaqt: 1000 msSizga N burchakli muntazam ko’pburchak berilgan, siz unga N – 3 ta kesishmaydigan dioganallar o’tkazishingiz kerak. Sizning vazifangiz bu dioganallarni necha xil usulda o’tkazish mumkin ekanligini aniqlashdan iborat. Bu son juda katta bo’lib ketishi mumkin shuning uchun qiymatini 1000000007 ga bo’lgandagi qoldiqni javob sifatida chiqarishingiz so’ralyapti.
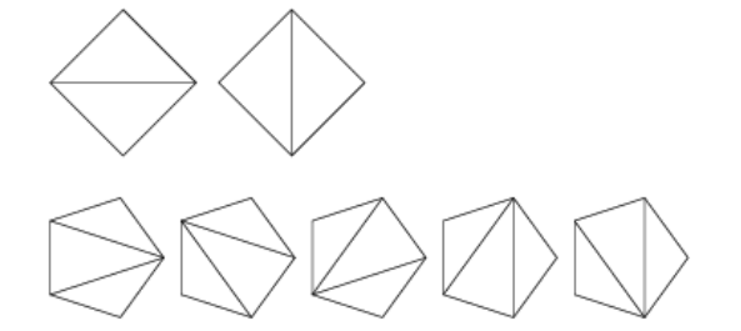
Yuqorida berilgan rasmda 4 va 5 burchakli muntazam ko’pburchaklar uchun natijalar ko’rsatilgan.
Bitta qatorda N soni beriladi \(( 3 < N < 1000)\)
Masalaning javobini \(1000000007\) ga bo’lgandagi qoldiqni toping
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
4 |
2 |
| 2 |
5 |
5 |
F. Oraliqdagi massiv.
Xotira: 16 MB, Vaqt: 1000 msBir o`lchamli sonli massiv [a,b] qismidagi elеmеntlari massivni eng kichik elеmеntiga bo`lib chiqilsin qolganlari o’zgartirishsiz qoldirilsin.
Birinchi satrda n\(( 1 \le n \le 100)\) .
Ikkinchi satrda C[i] massiv elementlari \((1 \le C[i] \le 10^9)\) butun sonlar kiritiladi.
Uchinchi satrda a va b oraliqlar \((1 \le a,b \le n)\) kiritiladi.
n ta son masala yechimlari probel bilan ajratilgan holda. Yechimlari \(10^{-1}\) aniqlikda chiqaring
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
4 44 99 55 12 1 3 |
3.7 8.3 4.6 12.0 |
G. Noodatiy dasturlash musobaqasi
Xotira: 16 MB, Vaqt: 1000 msNoodatiy dasturlash musobaqasida \(N\) ta o'quvchi ishtirok etmoqda. Uning boshqa musobaqalardan farqi shundaki bu musobaqa bir nechta raunddan tashkil topgan bo'ladi. Bunda masalani birinchi bo'lib ishlagan o'quvchi \(N\) ballni undan keyingilar mos ravishda 1 balldan kam ball olib boradi va har bir o'quvchi berilgan masalalarni ishlay olishi kafolatlanadi. Oxirgi bo'lib ishlagan ishtirokchi mos ravishda 1 ballni qo'lga kiritadi. Hozir sizga o'sha \(N\) nafar o'quvchining oxirgi raund oldidan ballari beriladi. Ulardan nechtasida g'oliblikni qo'lga kiritish imkoniyati borligini aniqlang.
Hech bir ikki o'quvchi bir vaqtda masalani ishlay olmaydi.
Agarda bir nechta o'quvchilarda ballar teng bo'lsa ularning barchasi g'olib deb topiladi.
Kirish faylining 1-qatorida \(N(3 \le N \le 300 000)\) soni kiritiladi.
Keyingi \(N\) qatorda o'quvchilarning oxirgi raungacha to'plagan ballari.
Bunda ularning qiymatlari nomanfiy butun sonlar hamda 2000000 dan oshmaydi.
Chiqish faylida yagona butun son nechta o'quvchida g'olib bo'lish imkoniyati borligini chop eting.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
3 8 10 9 |
3 |
| 2 |
5 15 14 15 12 14 |
4 |
H. Ketma-ketlik oxirgi raqam
Xotira: 16 MB, Vaqt: 1000 msJahongir ketma-ketliklarga qiziqadi. Bir kuni u ustozi bergan ketma-ketlik qaysi qonuniyat asosida ketishini aniqlash va shu ketma-ketlikning n-hadini oxirgi raqamini topish kerak edi. Jahongir qonuniyatni topdi! Qonuniyat shundan iborat ediki ketma-ketlikning dastlabki 3ta hadi beriladi. keyingi har bir had o'zidan oldingi 3ta hadning yig'indisiga teng. Endi sizning vazifangiz shu qonuniyat asosida ketma-ketlikning n-hadini topib Jahongirga yordam berishdan iborat
Birinchi qatorda probel bilan ajratilgan holda 3ta butun son a, b, c va keyingi qatorda q butun sonlari kiritiladi. Keyingi qatorda probel bilan ajratilgan holda q ta butun son probel bilan ajratilgan holda kiritiladi. \((1 \leq a, b, c \leq 10^{18}, 0 < q \leq 1000, 1 \leq n \leq 10^{18})\)
Chiqish faylida bitta qatorda q ta so'rov uchun ketma-ketlikning n-hadning oxirgi raqami probellar bilan ajratilgan holda chiqarilsin.
a-had ketma-ketlikning 0-hadi hisoblanadi
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
1 4 8 6 4 5 6 7 8 9 |
5 6 4 5 5 4 |
I. Oxirgi yig'indi
Xotira: 256 MB, Vaqt: 2000 msBu masalada sizga \(N\) o'lchamli \(A\) massiv berilgan. Siz esa uni oxirgi elementi qolguncha quyidagi amalni bajarishingiz kerak bo'ladi. Misol uchun sizga 5 ta elementdan iborat quyidagi massiv berilsa\( [1,2,3,4,5]. [1+2,2+3,3+4,4+5]\) va keyin\( [3,5,7,9] \)massivi hosil qilinadi. So'ng yana\( [3+5,5+7,7+9] = [8,12,16]\). Bu amal toki massiv elementi bitta qolguncha davom etadi. \([8+12,12+16] = [20,28]\) va oxirida \([20+28]\) qoladi. Shunda natija \(48\)teng bo'ladi. Siz ham sizga berilgan massivni oxirgi elementi qolguncha shu amallarni ketma - ket bajarib borasiz. Eng oxirida qolgan elementni ekranga chiqarishingiz kerak bo'ladi.
Birinchi qatorda \(N\) soni \(N(3≤N≤10^6).\)
Ikkinchi qatorda \(N \) ta sondan iborat \(A\) massiv \(A[i] (1≤ A[i]≤10^9).\)
Yagona qatorda masala yechimini ekranga chiqaring.
Masala yechimi juda katta bo'lib ketishi mumkin shuning uchun uni \(10^9+7\) ga bo'lgandagi qoldiqni ekranga chiqarishingiz kerak bo'ladi.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
5 1 2 3 4 5 |
48 |
J. Maxsus sovg'a
Xotira: 256 MB, Vaqt: 2000 msQorbobo sizga juda injiq bola uchun sovg'a tayyorlashni buyurdi. Bola sovg'a sifatida ko'pi bilan \(N\) ta shar olishni xohlaydi, lekin u injiqligi tufayli hamma sharlari och rangli bo'lib qolishini xohlamaydi, xuddi shunday to'q rangli bo'lib qolishini ham xohlamaydi. Sizga Qorbobo \(K\) xil rangdagi sharlarning har biridan cheksiz miqdorda ishlatishga ruxsat berdi. Siz sovg'a bolaga yoqishi uchun quyidagicha usulda sovg'ani tayyorlashingiz kerak:
- \(K\) xil shardan 1 tadan \(N\) tagacha qilib yasash mumkin bo'lgan barcha turli sharlar to'plamini yasab chiqasiz va ularni och ranglardan to'qga qarab saralaysiz. (Leksikografik saralashga o'xshash, aniqroq tushunish uchun namunaviy test va uning izohini tekshiring)
- Tasavvur qiling sizda \(S\) ta sovg'a (sharlar to'plami) hosil bo'ldi. Siz bolaga sovg'a sifatida \(\frac{S}{2}\) - sovg'ani berasiz, chunki bu sovg'a ranglar jihatidan muvozanatlangan bo'ladi.
Bolaga berilgan sovg'adagi sharlar ranglarini chiqaring.
E'tibor bering: To'plamda bir nechta bir xil rangdagi sharlar bo'lishi mumkin.
\(N\) va \(K\) natural sonlari: \(1 \leq N, K \leq 3*10^5\)
Masala javobini chiqarishda ranglarni sonlar bilan ifodalang. Bunda 1 soni eng och rangga, \(K\) soni eng to'q rangga mos keladi.
1-test uchun izoh:
Yasash mumkin bo'lgan to'plamlar: (1), (1,1), (1,2), (2), (2,1), (2,2)
6/2=3 - eng kichik to'plam (1,2).
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
2 2 |
1 2 |
| 2 |
2 3 |
2 1 |
K. Chess
Xotira: 16 MB, Vaqt: 1000 ms Ushbu masalada sizga \(8\times8\) maydonda bo'lib o'tadigan standart shaxmat o'yinining qaysidur jarayoni beriladi. Bu jarayonda yurish navbati sizga kelib qolgan va usha jarayonda faqatgina bitta yurish bilan raqibni mot qilishingiz kerak bo'ladi.
Ushbu masalada sizga \(8\times8\) maydonda bo'lib o'tadigan standart shaxmat o'yinining qaysidur jarayoni beriladi. Bu jarayonda yurish navbati sizga kelib qolgan va usha jarayonda faqatgina bitta yurish bilan raqibni mot qilishingiz kerak bo'ladi.
Misol: Agar siz oq toshlarda o'ynayotgan bo'lsangiz C5 da joylashgan ot ni D7 ga olib o'tish orqali raqibni bir marotaba yurishda mot qilish mumkun(1-test).
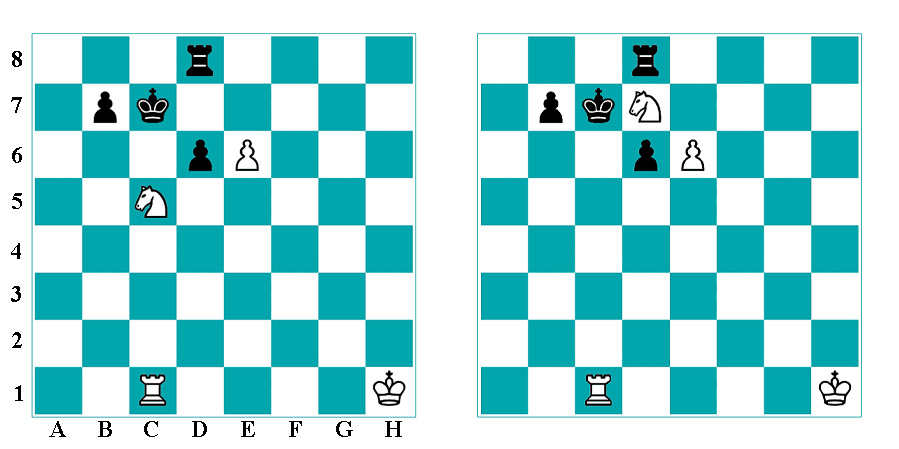
Shaxmat tosh donalari quyidagicha belgilanadi: King(shox) - K, Queen(farzin) - Q, Bishop(fil) - B, Knight(ot) - N, Rook(rux) - R va Pawn(piyoda) - P. Oq va qora toshlar mos ravishda katta kichik harflar bilan va bo'sh maydon nuqta bilan ifodalanadi.
Kirish faylining dastlabki satrida \(k(0\leq k\leq 1)\) butun son ya'ni 0 yoki 1 bu mos ravishda siz o'yinni qora yoki oq toshlarda davom ettirishingizni anglatadi. Kiyin \(8\times8\) maydonda o'yin jarayoni tasvirlanadi.
Siz shunday bir toshni boshqa maydonga kuchirish orqali shoxga hujum qilishingiz kerak natejada shox hujum ostida qolsin. Ko'chirilishi kerak bo'lgan toshning dastlabki va kiyingi koordinatasini mos ravishda probil bilan ajratilgan holda(agar bunday yechimlar bir nechta bo'lsa istalganini) chop eting. Yechim mavjudligi kafolatlanadi.
Piyoda harakati siz oq yoki qora toshlarda o'ynashingizdan qati nazar faqat bir tomonlama bo'ladi 2-testga qarang.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
1 ...r.... .pk..... ...pP... ..N..... ........ ........ ........ ..R....K |
C5 D7 |
| 2 |
0 ....K.R. .Pp..P.P ....Bb.. ..pP.... R.....p. .......p ....r... .......k |
C7 C8 |