A. XOR
Xotira: 16 MB, Vaqt: 1000 msBiz yangicha fibonachchi sonlarining turini ishlab chiqdik, u quyidagicha hosil qilinadi. Avvaliga \(K\) ta son olinadi, demak fibonachchining dastlabki \(K\) ta elementi shular ya’ni quyidagicha:
\(F(1) = a_1, F(2) = a_2, \space F(3) = a_3, \space\dots\space, \space F(k) = a_k\)
Qolgan elementlari esa o`zidan oldingi K tasining umumiy xoriga teng ya’ni quyidagicha:
\(F(i) = F(i−1) \space\text{xor}\space F(i−2) \space\text{xor}\space F(i-3) \space\text{xor}\space … \space\text{xor}\space F(i-k), \space (\text{qachonki} \space i > k)\)
Demak sizga yangicha Fibonachchi ketma-ketligimiz tushunarli bo`lsa sizning vazifangiz \(L\) va \(R\) oraliqdagi barcha fibonachchi sonlarimizni umumiy xor qiymatini hisoblab berishingiz talab qilinadi ya’ni quyidagicha:
\(F(L) \space\text{xor}\space F(L+1) \space\text{xor}\space F(L+2) \space\text{xor}\space … \space\text{xor}\space F(R-1) \space\text{xor}\space F(R)\)
Birinchi qatorda \(K \space (1 \le K \le 10^5)\) butun son fibonachchining dastlabki elementlari soni.
Keyingi \(K\) ta qatorda \(A_i (0 \le A_i \le 10^{18})\) butun sonlar son fibonachchining dastlabki elementlari beriladi.
Keyingi qatorda \(Q (1 \le K \le 10^6)\) soni so`rovlar soni.
Keyingi \(Q\) ta qatorda \(L\) va \(R (1 \le L \le R \le 10^{18})\) har bir so`rovdagi \(L\) va \(R\) siz hisoblab berishingiz kerak bo`lgan oraliq.
\(Q\) ta alohida qatorda yagona butun \(L\) va \(R\) oraliqdagi biz tuzgan yangi Fibonachchi ketma-ketligining sonlarini umumiy xor qiymatini chiqaring
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
4 1 3 5 7 3 2 2 2 5 1 5 |
3 1 0 |
| 2 |
5 3 3 4 3 2 4 1 2 1 3 5 6 7 9 |
0 4 7 4 |
B. Alien
Xotira: 16 MB, Vaqt: 1000 msYaqinda kosmik kemamiz boshqa gallaktikadagi yerga o`xshash sayyoraga borib qo`ndi, bu yerda ham tirik mavjudod bor ekan, baxtga ko`ra ular ham idrok etish va hatto musiqa kuylab pianino chalishni yaxshi ko`rishar ekan. U yerdagilardagi o`zgacha xususiyat ularda qo`l barmoqlari aynan 10 ta emas ekan hammada har xil, \(K\) ta ekan, bizni yangicha pianinoda esa \(N\) ta klavish bo`lib har bir klavishni o`zining yangicha xususiyati bor, har bir klavishda aniq bir tovush \(A_i\) balandligi bor ba’zilarining tovush balandligi bir xil, agar siz 2 ta bir xil balandlikdagi tovush chiqaradigan klavishni bossangiz ixtiyoriy biri ovoz chiqaradi, ammo 2 ta turli xil ovozdagini bossangiz faqat baland ovozlisi ovoz chiqaradi, bu holat bir nechta klavishni bosganda ham shunday, endi biz o`zga sayyorlik do`stimizga shu holatda har doim har xil usuldagi urunishlarni hamma barmoqlari bilan tengidan klavishlarni bosganida umumiy tovush balandligining yig`indisi qancha bo`lashini so`ragandik, u buni hisoblab bera olmadi, endi siz ularni mushkulini yengillashtirish uchun bizga dastur tuzib yordam bering.
Yagona qatorda \(N\) va \(K\) \((1 \le N \le 10^5, 1 \le K \le 50)\) butun sonlari beriladi mos ravishda bizning pianinodagi klavishlar soni va o`zga sayyoralikning barmoqlari soni.
Keyin qatorda \(N\) ta butun \(A_i (0 \le A_i \le 10^9)\) sonlari klavishlarning ovoz balandligi beriladi.
Yagona butun son masala yechimini \(10^9+7\) ga bo`lgandagi qoldiqni chiqaring.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
5 3 2 4 2 3 4 |
39 |
| 2 |
5 1 1 0 1 1 1 |
4 |
C. Min-Max
Xotira: 32 MB, Vaqt: 1000 ms\(L\) va \(R\) oraliqdan shunday eng kichik va eng katta sonlarni topingki har ikkilasining ham raqamlari yig`idisi \(N\) ga teng bo`lsin.
Har biri alohida qatorda \(L, R \space \text{va} \space N \space (0 < L \le R \le 10^4, 0 \le N \le 36)\) butun sonlari beriladi.
Yechim borligi kafolatlanadi.
Har biri alohida qatorda eng kichik va eng katta sonlarni chiqaring.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
1 20 5 |
5 14 |
| 2 |
100 200 10 |
109 190 |
D. Reverse-Sort
Xotira: 32 MB, Vaqt: 1000 ms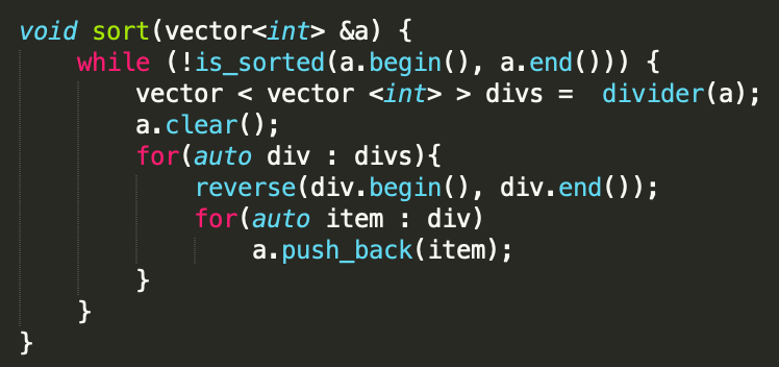
Vectorni saralashda biz ushbu metodni ishlatamiz bu yerda ishlatilayotgan divider() metodi vectorni eng kam sondagi kamayuvchi qism massivlarga bo`lib beradi, bu funksiyani birinchi marta chaqirilganda undan qaytgan qism massivlar uzunligi juft bo`ladi, bu holat faqat birinchi marta chaqirilganda, reverse() metodi vectorni teskarisiga o`girib beradi.
Sizga \(N\) ta elementda iborat \(A\) vector berilgan, vector elementlari \(1\) dan \(N\) gacha bo`lgan sonlarning qaysidir permutatsiyasi, siz vectorni bizning sort() metodimiz orqali saralaganingizda eng kamida necha marta reverse() metodi chaqiriladi.
Birinchi qatorda \(N (2 \le N \le 10^5)\) butun son massiv elementlari soni beriladi.
Keyingi qatorda \(N \space \text{ta} \space A_i ( 1 \le A_i \le N)\)butun sonlar massiv elementlari beriladi.
Yagona butun son masala yechimini chop eting!
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
4 4 3 2 1 |
1 |
E. Make-String
Xotira: 512 MB, Vaqt: 2500 msSizga \(N\) uzunlikda \(S\) satr beriladi. Sizning vazifangiz ushbu satrdan yana bir nusxa tayyorlash, buning uchun sizga \(M\) ta \(L_i\) \((1 \le i \le M)\) satrchalar borligi aytiladi, bu satrchalar cheksiz ko`p. Siz \(S\) satrni \(M\) xil satrlar yordamida qayta yozishingiz kerak bunda \(L_i\) satr bilan \(L_j (1 \le i \le M, 1 \le j \le M, i \space \text{va} \space j \space \text{bir xil bo`lishi mumkin})\) satrni faqat o`xshash harflarini ustma – ust qo`yish yordamida birlashtirishingiz yoki satrlarni ketma-ket joylashtirishingiz mumkin. Satrlarning tartibi buzilishiga ham ruxsat etilgan ammo satrlarni bo`laklash yoki teskarisiga o`girish mumkin emas.
Sizning vazifangiz \(S\) satrdan eng kam nechta belgini qayta tiklay olmasligingizni aniqlash. Unutmang siz hosil qiladigan satr \(N\) dan oshmasligi kerak!
Birinchi qatorda \(N (1 \le N \le 3*10^5)\) butun son satr uzunligi.
Ikkinchi qatorda \(S\) satr beriladi.
Uchinchi qatorda \(M (1 \le M \le 5000)\) butun soni satrchalar soni
Keyingi \(M\) ta qatorda \(L_i (1 \le L_i \le 5000)\) satrchalar beriladi.
Barcha satrlardagi belgilar lotin kichik harflaridan iborat.
Yagona butun son masala yechimini chop eting!
1 – testda siz \(\text{abr+kada+\textcolor{red}{\text{a}}br+kada+\textcolor{red}{\text{a}}br}\) tartibda
natijada : \(\text{abr\{a\}kadabr\{a\}kadabr\{a\}}\)
Siz eng kamida 3 ta belgini hosil qilolmaysiz bular gulli qavs ichidagi \(a\) harflari
2 – testda siz \(\text{abra+kada+\textcolor{red}{a}bra+kada+\textcolor{red}{a}bra}\) tartibda
natijada : \(\text{abrakadabrakadabra}\)
Satrni to`liq hosil qilishingiz mumkin!
Izohlardagi qizil rangdagi harflar 2 marta yozilgan bunda ular ustma – ust qo`yilganini bildiradi.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
18 abrakadabrakadabra 3 abr kada kobra |
3 |
| 2 |
18 abrakadabrakadabra 3 abra kada kobra |
0 |