A. Tublar yigʻindisi

Xotira: 16 MB, Vaqt: 1000 ms

Masala

Sizga N soni beriladi. Bu sonni 2 ta tub son yigʻindisi koʻrinishida necha xil usulda ifodalash mumkin.

Kiruvchi ma'lumotlar:

Kirish faylida bitta butun son \(N ( 1 ≤ N ≤ 10^5)\) kiritiladi

Chiquvchi ma'lumotlar:

Chiqish faylida tub sonlar juftligi sonini chop eting

Izoh:

N = 14,

3 + 11 = 14
7 + 7 = 14
11 + 3 = 14

14 ni 3 xil usulda ifodalash mumkin

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	14	3

B. Uchburchakli sonlar 3

Xotira: 16 MB, Vaqt: 1000 ms

Masala

Uchburchakli sonlar haqida hammamiz eshitganmiz. Bu 1 dan n gacha boʻlgan n ta natural sonning yigʻindisiga teng miqdorda nuqtadan iborat uchburchak. Sizning vazifangiz n ta uchburchakli sonlar yigʻindisini \(10^9 + 7\) ga boʻlgandagi qoldiqni topishdan iborat.

Kiruvchi ma'lumotlar:

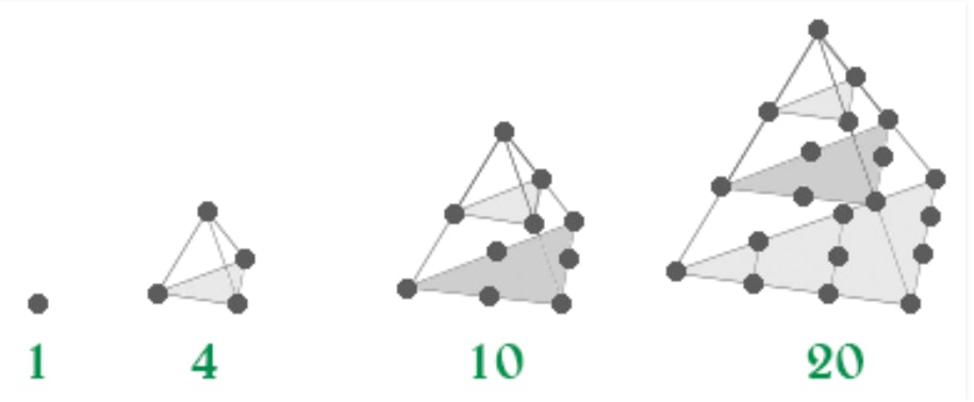
Kirish faylida yagona butun son \(n (1 ≤ N ≤ 10^{18})\)soni kiritiladi.

Chiquvchi ma'lumotlar:

Yigʻindining \(10^9 + 7\) ga boʻlgandagi qoldigʻini chiqaring

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	2	4

C. Uchliklar 1

Xotira: 16 MB, Vaqt: 1000 ms

Masala

Uzunligi \(n\) ga teng massiv beriladi. \(i < j < k\) va \(a[i] < a[j] < a[k]\) shartni qanoatlantiradigan \(\text{max} ( a[i] + a[j] + a[k] )\) ni toping.

Masalan \(n = 6\) boʻlganda , \(A= \{ 3 , 7 , 4 , 2 , 9 , 2 \}\), \(\text{max} ( 9 + 7 + 3 ) = 19\)

Kiruvchi ma'lumotlar:

Kirish faylida \(n ( 3 ≤ n ≤ 10^3 )\) soni. Keyingi qatorda \(n\) ta butun son massiv elemetlari kiritiladi. Massiv elementlari \(10^9\) dan oshmasligi kafolatlanadi.

Chiquvchi ma'lumotlar:

Yagona butun son maksimal uchlikni chop eting

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	4 2 3 1 5	10

D. Uchliklar 2

Xotira: 16 MB, Vaqt: 1000 ms

Masala

Uzunligi n ga teng massiv beriladi. \(i < j < k\) va \(a[i] > a[j] > a[k]\) shartni qanoatlantiradigan uchliklar sonini toping.

Masalan \(n = 6\) boʻlganda, \(A= \{ 3 , 9 , 7 , 5 , 3 , 7 \}\)

Uchliklar soni 4 ta,

9 7 5
9 7 3
9 5 3
7 5 3

Kiruvchi ma'lumotlar:

Kirish faylida \(n ( 3 ≤ n ≤ 500 )\) soni. Keyingi qatorda \(n\) ta butun son massiv elemetlari kiritiladi. Massiv elementlari \(10^9\) dan oshmasligi kafolatlanadi.

Chiquvchi ma'lumotlar:

Yagona butun son uchliklar sonini chop eting.

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	4 4 3 2 1	4

E. Ikkilik nisbat

Xotira: 16 MB, Vaqt: 500 ms

Masala

Bobur sanoq sistemalariga juda ham qiziqadi ammo yaxshi bilmaydi. Bir kuni u informatika darsida o'tirganida ustozi unga savol berdi.
Savol shundan iboratki, Boburga \(n\) soni berildi. Unga sonning ikkilik sanoq sistemasidagi birlar sonini nollar soniga nisbatini topish kerakligi aytildi. Afsuski, Bobur misolni ishlashda qiyinchiliklarga duch keldi. Keling unda siz Boburga yordam bering.

Kiruvchi ma'lumotlar:

Kirish faylining yagona satrida bitta \(n\) natural son \((n ≤10^{18})\)

Chiquvchi ma'lumotlar:

Chiqish faylida so’ralgan javobni butun qismini chiqaring, agar buning iloji bo'lmasa ekranga \(-1\) ni chiqaring.

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	4	0
2	17	0

F. Murakkab tenglama

Xotira: 16 MB, Vaqt: 1000 ms

Masala

\(ax^3+bx^2+cx+d=0\) ko'rinishidagi tenglama berilgan bo'lsin. Biz 3-darajali tenglamani kamida bitta butun ildizga ega bo'lgan paytida Murakkab tenglama deb atashimiz mumkin.Sizga \(a,b,c,d\) sonlar berilgan bo'lsa \((a ≠ 0)\), ushbu matematik ifoda Murakkab tenglama bo'la oladimi yoki yo'qligini aniqlashdan iborat.

Kiruvchi ma'lumotlar:

Kirish faylining yagona satrida \(4\) ta butun sonlar \((-10^{12} ≤ a,b,c,d ≤ 10^{12})\) kiritiladi.

Chiquvchi ma'lumotlar:

Chiqish faylida agar tenglama "Murakkab tenglama" bo'lsa "Yes", aks holda "No" so'zini chiqaring.

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	1 2 3 2	Yes
2	1 0 0 0	Yes

G. G'alati ketma-ketlik

Xotira: 16 MB, Vaqt: 500 ms

Masala

Sizga quyidagi ketma-ketlik berilgan:
1, 8, 22, 43, 71, ...
Ketma-ketlikning \(n\)-hadini toping.

Kiruvchi ma'lumotlar:

Kirish faylining yagona satrida \(n\) soni \((n≤10^8)\) kiritiladi.

Chiquvchi ma'lumotlar:

Chiqish faylida masala javobini chiqaring.

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	1	1
2	2	8

H. Maximum son 2

Xotira: 16 MB, Vaqt: 1000 ms

Masala

Lazizda \(n\) ta son bor edi. U bu sonlarni yonma-yon qo’ygan holda eng katta son hosil qilmoqchi. Lekin bu ishni bir o’zi eplay olmaydi. Siz unga bu muammoni yechishda yordamlashing.

Kiruvchi ma'lumotlar:

Kirish faylining dastlabki qatorida \(n(2 ≤ n ≤ 100)\) soni kiritiladi. Keyingi \(n\) ta qatorda nomanfiy va qiymati \(10^{30}\) dan oshmaydigan sonlar berilgan.

Chiquvchi ma'lumotlar:

Chiqish faylida masalani javobi chiqarilsin.

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	5 2 9 5 3 5	95532

I. Matematik Shoxjaxon

Xotira: 32 MB, Vaqt: 1000 ms

Masala

Shoxjaxon matematikaga juda qiziqadi. Shu sababli u do’stlariga ham yordamlashib turadi. Shoxjaxonning jami \(n\) nafar do’sti bor. U do’stlariga \(a[i]\) ta misol ishlab berishi mumkin. Do’stlari ko’pligi sababli u boshqacha yo’l tutdi. U bitta do’stini misolini ishlab berganidan so’ng shu do’stinikidan ko’p bo’lgan boshqa do’stini misolini ishlab berishi mumkin ya’ni \(a[i] < a[j] < a[k], …\) tartibida bo’lishi shart. Shunday qilib u eng ko’pi bilan nechta do’stiga yordam berishi mumkin.

Kiruvchi ma'lumotlar:

Kirish faylida birinchi qatorda Shoxjaxonning do’stlari soni \((2 ≤ n ≤ 2500)\). Keyingi qatorda \(n\) ta son \((0 ≤ a[i] ≤ 10000)\) kiritiladi.

Chiquvchi ma'lumotlar:

Chiqish faylida masalani javobi chiqarilsin

Izoh:

1 – testga izoh:

Jami 8 nafar do’sti bor va ularning misollari soni keltirilgan. Shoxjaxon bu holatda 5 nafariga yordam bera oladi ya’ni: \([0, 3, 7, 8, 9]\). Bunda sonlar qatiy o’suvchi ketma-ketligida bo’lishi shart

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	8 4 0 3 2 7 1 8 9	5

J. Koptokchalar o’yini

Xotira: 128 MB, Vaqt: 1500 ms

Masala

Shoxjaxon va Laziz karantinda zerikib qolmaslik uchun navbatma-navbat o'yin o'ynab turishadi. Bir kuni ular antiqa o‘yin o‘ylab topishdi. O‘yin sharti quyidagicha: Bir qatorda joylashgan \(n\) ta koptokchalar bor. Har bir koptokcha o’z raqamiga ega va bir qatorda joylashtirilgan. Har bir o'yinchi o'z navbatida chap tarafda joylashgan koptokchani yoki o'ngda joylashgan koptokchani qatordan olib tashlashlari va qatordagi qolgan koptokchalarning qiymatlari yig'indisiga teng ball olishlari mumkin. Olib tashlash uchun toshlar qolmaganda, yuqori ball to'plagan g'olib hisoblanadi. Birinchi bo'lib o’yinni Shoxjaxon boshlaydi. Laziz har doim bu o'yinda yutqazishini aniqladi, shuning uchun u hisobdagi farqni minimallashtirishga qaror qildi. Shoxjaxonning maqsadi esa hisobdagi farqni maksimal darajada oshirish. Agar ikkalasi ham optimal darajada oʻynasa, Shoxjaxon va Lazizning yig’gan ballaridagi orasidagi farqni topib berishga yordamlashing.

Kiruvchi ma'lumotlar:

Kirish faylida bitta butun son \(3 ≤ n ≤ 1000\) kiritiladi. Keyingi qatorda \(n\) ta butun son, qiymati 1000 dan oshmaydi

Chiquvchi ma'lumotlar:

Chiqish faylida Shoxjaxon va Lazizning yig’gan ballaridagi orasidagi minimal farqni chop eting.

Izoh:

1-testga izoh: \([ 1, 2, 10, 5, 3]\) kiritiladi.

Shoxjaxon 1 ni olib tashlaydi va ularning yig’gan ballari 2+10+5+3=20 ball. Shoxjaxon=20, Laziz=0. \([2,10,5,3]\)

Laziz 2 ni olib tashlaydi va ularni yig’gan ballari 10+5+3=18 ball. Shoxjaxon=20, Laziz=18. \([10,5,3]\)

Shoxjaxon 3 ni olib tashlaydi va ularning yig’gan balllari 10+5=15 ball. Shoxjaxon=35, Laziz=18. \([10,5]\)

Laziz 5 ni olib tashlaydi va ularni yig’gan ballari 10 ball. Shoxjaxon=35, Laziz=28. \([]\)

Ularning ballari orasidagi farqi esa 35 – 28 = 7 ball

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	5 1 2 10 5 3	7