Masala G
Azimjon va daraxt
Azimjon daraxtlar dunyosiga chuqurroq nazar solishga qaror qildi. U tabiatni matematika tili orqali tushunmoqchi edi.
Faraz qiling, Azimjon daraxtni graf sifatida ifodalaydi: bu grafda
- uchlar (tugunlar) — daraxtning shoxlari,
- qirralar esa — ularni bog‘lovchi yo‘llardir.
Agar daraxtda \(n\) ta uch bo‘lsa, u holda qirralar soni \(n-1\) bo‘lishi aniq — chunki bu graf daraxt (ya’ni, ulanma va siklsiz).
Endi Azimjon shunday savol ustida bosh qotirmoqda:
Daraxtdagi shunday ikkita uchi topilsinki, ular orasidagi eng katta masofa mavjud bo‘lsin.
Kirish faylining dastlabki satrida \(n(2\leq n\leq 10^5)\) butun soni, daraxt uchlari soni. Kiyingi \(n-1\) ta satrda \(u_i,v_i(1\leq u_i, v_i\leq n;u_i\neq v_i)\) juftliklar, ikki uch o'rtasida qirra mavjudligini ifodalaydi. Berilgan ma'lumotlarda daraxt berilishi kafolatlanadi.
Chiqish faylida daraxtning shunday ikki uchini chop etingki, ushbu uchlar o'rtasidagi masofada maksimal sondagi qirralar mavjud bo'lsin. Javoblar bir nechta bo'lsa istalgan javobni chop etishingiz mumkin, istalgan tartibda \((u,v)\) yoki \((v, u)\) ko'rinishida.
| # | input.txt | output.txt |
|---|---|---|
| 1 |
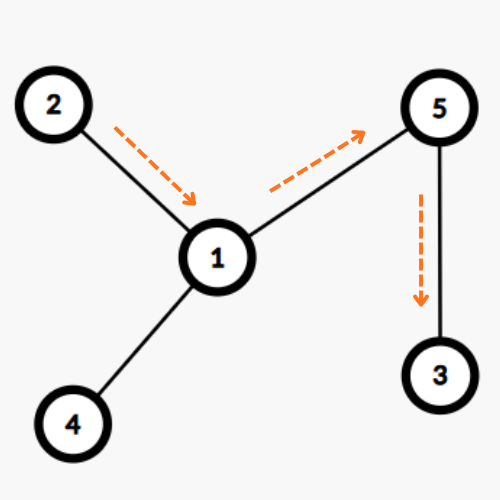
5 1 2 1 4 1 5 5 3 |
2 3 |
Birinchi testda bir nechta javoblar mavjud \((2,3)\), \((3, 2)\), \((3, 4)\) va \((4,3)\)