Masala #K9PE0WYF62
To'rtburchaklar bilan qoplangan umumiy maydon
Ushbu Masalani bajarish uchun sizning vazifangiz to'rtburchaklar birlashmasi bilan qoplangan maydonni hisoblaydigan funktsiyani yozishdir.
To'rtburchaklar bo'sh bo'lmagan kesishmalarga ega bo'lishi mumkin, shu tarzda oddiy yechim: Sall = S1 + S2 + ... + Sn-1 + Sn (bu erda n - to'rtburchaklar miqdori) ishlamaydi.
Old shartlar
har bir to'rtburchak quyidagicha ifodalanadi: [x0, y0, x1, y1]
(x0, y0) - pastki chap burchakning koordinatalari
(x1, y1) - yuqori o'ng burchakning koordinatalari
xi, yi - musbat butun sonlar yoki nollar (0, 1, 2, 3, 4..)
to'rtburchaklar tomonlari koordinata o'qlariga parallel
sizning kiritilgan ma'lumotlaringiz to'rtburchaklar qatoridir
Talablar
Bitta testdagi to'rtburchaklar soni (oddiy testlarni hisobga olmaganda) 3000 dan 15000 gacha. Bunday diapazonga ega 10 ta test mavjud. Shunday qilib, sizning algoritmingiz optimal bo'lishi kerak.
To'rtburchaklar o'lchamlari 1e6 kabi qiymatlarga yetishi mumkin.
Bir nechta sonlar jamlanmasi beriladi, bo'sh bo'lishi ham mumkin
Masalada so'ralgan javobni chop eting
| # | input.txt | output.txt |
|---|---|---|
| 1 |
0 4 11 6 |
22 |
| 2 |
0 0 1 1 1 1 2 2 |
2 |
| 3 |
3 3 8 5 6 3 8 9 11 6 14 12 |
36 |
Masalan:
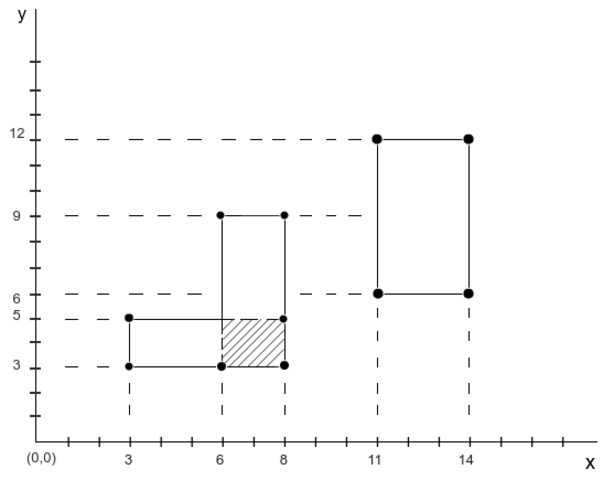
Uchta to'rtburchaklar mavjud:
R1: [3,3,8,5], maydoni 10
R2: [6,3,8,9], maydoni 12
R3: [11,6,14,12], maydoni 18
R1 va R2 bir-birining ustiga chiqadi (2x2), kulrang maydon umumiy maydondan chiqariladi
Demak, umumiy maydon 10 + 12 + 18 - 4 = 36 ga teng
Telegram kanalimizga obuna bo'ling